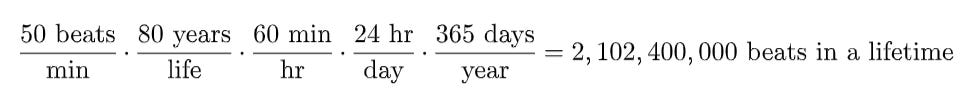Boise State Math Outreach Updates - January, 2023
POM #4 Recap & Winner! | The Pop Culture / Mathematics Venn Diagram | POM #5 - Estimation Explication
Problem of the Month #4 Recap & Winner!
Conditionality is such an important principle in mathematics. The sum of the squares of the legs of a triangle is equal to the square of the hypotenuse … if the triangle is right. The probability of event A or event B is the sum of their probabilities … if the events are disjoint. There’s an abundance of other examples.
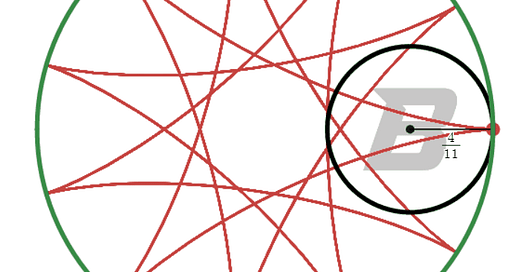
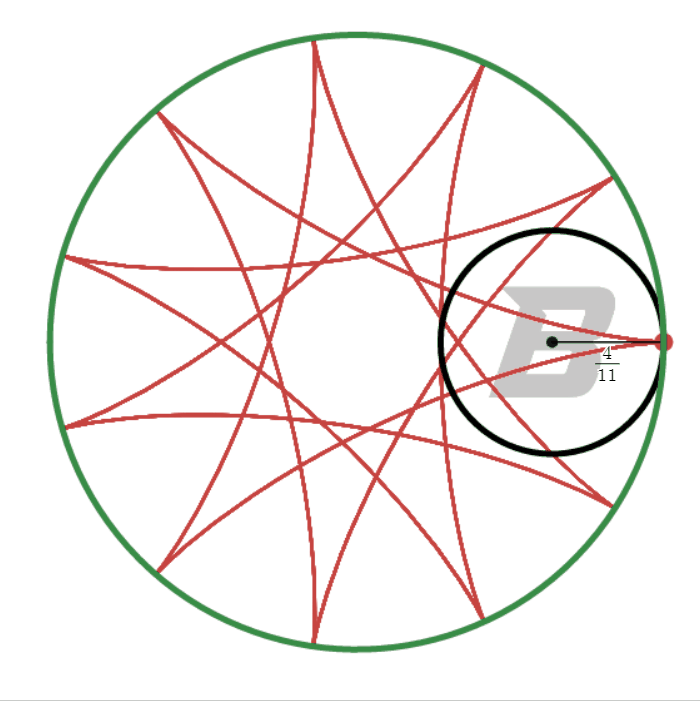
Circles in Circles (POM #4) was written in part to make pretty pictures of hypocycloids, but also to force students to think about conditions. The relatively closed nature of the solution merits a quick discussion, so you can read about it at this link. (Archives of past problems are always available at the Boise State Mathematics Outreach page.)
The winning submission came from Daniel Yang at the Treasure Valley Mathematics and Science Center magnet school in the Boise School District. Daniel is in Mr. Erwin’s class at TVMSC, and his home school is Lowell Scott Middle School in the West Ada School District. His write-up was detailed with rich, descriptive images and explanations.

Last month’s participants were also given access to a (still active) Desmos Classroom activity designed to help visualize the problem. In the spirit of the holiday season, I made the first screen an ugly sweater contest, and Elsa Papenfuss in Colby Crenshaw’s class at Owyhee High School in the West Ada School District will receive a Boise State sticker for this amazing contribution.
This month’s problem, Estimation Explication, appears below, and winning may involve a little bit of luck. Submissions are due February 17th, so get started now!
The Pop Culture / Mathematics Venn Diagram
For the past decade, I have been fascinated by the strange juxtaposition of traditional school mathematics education and what I’ll call ‘math-u-tainment’ on the Internet generally and, more recently, on social media, with Howey Hua, blackpenredpen, and Calculuscious racking up thousands of followers on TikTok and Instagram. Obviously, we all agree that this is perhaps the most pressing issue facing education, nay America! So let’s devote part of this newsletter to analyze it.
When I saw my first Numberphile video in 2015 when a former student sent it my way, I immediately began incorporating their videos in my day-to-day teaching whenever I could. Those who follow the channel know that the topics covered are rarely taken directly from the standard secondary school curriculum, but there is often a tangential connection, like the use of the Intermediate Value Theorem to fix a wobbly table, or this unusual conceptualization of the Fundamental Theorem of Algebra. Often, though, the most entertaining videos are marginally (if at all) connected to secondary school mathematics, like my personal all-time favorite Numberphile submission: this excellent piece on strange attractors.
There are others, of course. Vi Hart, Matt Parker, ThreeBlueOneBrown, and Hannah Fry have each amassed millions of followers with their brands, and I devour them like samples at a 31 flavors of math. I can’t help but wonder, though: Why isn’t the product they’re selling translating into more sales at the checkout line of traditional schooling? After all, the skills K-12 teachers deliver every day are ultimately necessary to understand the mathematics they’re selling, right?
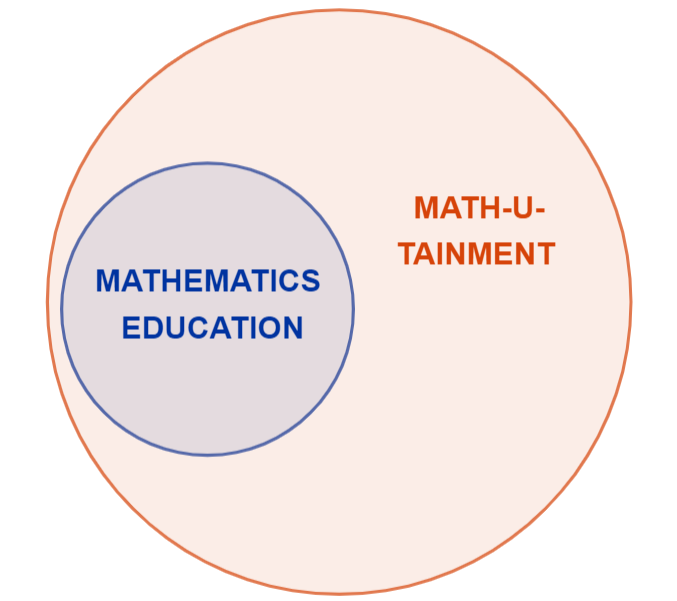
Truthfully, I think I know the reason, and it’s that the Venn diagram of mathematics education and ‘math-u-tainment’ looks something like …
… when it could very easily look like …
… but should perhaps look like …
… or maybe not. I’m sure you have an opinion.
Problem-of-the-Month #5 - Estimation Explication
Speaking of ‘math-u-tainment’, one of my favorite authors is Ben Orlin, the genius behind Math With Bad Drawings, and he wrote a fantastic piece about Fermi Questions, named after physicist, Enrico Fermi. (Unfamiliar with Ben’s books? I’m of the opinion that Change is the Only Constant should be required reading in first-year calculus courses.) In consideration of this, and with the springtime tradition of science bowls on the horizon, this month’s problem is devoted to the art and/or science of estimation.
For those unfamiliar or needing a refresher, the answers to Fermi Questions seem impossible, but estimations can be found using assumptions and deduction, with the answer given as a power of ten. (Here’s a good starting point to learn more.)
Example: How many beats does your heart make during your lifetime?
Necessary facts: Typical heart rate, typical life span of a human being.
Declare basic assumptions: Assume a resting heart rate of approximately 50 beats per minute (lots of time spent sleeping, offset by some periods of exercise.) Let’s assume a typical life span of 80-ish years.
Now we use these assumptions along with some basic facts to calculate:
Provide an answer in the form of a power of ten: Our calculation gives us roughly 2 billion, or 2 times 10^9 beats per lifetime, so we answer with just the power of ten: 9
(Disclosure: I googled the same question after writing that example. Same result!)
This month’s problem presents three locally significant Fermi Questions. For each question, explicate your estimate by stating assumptions and known facts, show your calculations that lead to your estimate, and provide the power of ten as your final answer. High score wins, based on the following traditional point system:
5 points for the correct power of ten.
3 points for one away from the correct power of ten.
1 point for two away from the correct power of ten.
What if there’s a tie? In the event of a tie, the submission with the closest guess to the number of books in my office wins. To be clear: This tiebreaker is not a Fermi Question. Just guess how many books are in my office.
Ready to get started? Click here to get estimating! Submissions are due by 11:59 PM on February 17th.